TIL Parallel Convolution with Tiling in GPUs
In the continued saga of “Subil learns how to program GPUs”, today I learned about convolution and how to program it for a GPU.
What is convolution? Well, I learned just enough so that I’m satisfied with how it works, but definitely not enough to explain it with any depth in this post. See this article or this video for explanations.
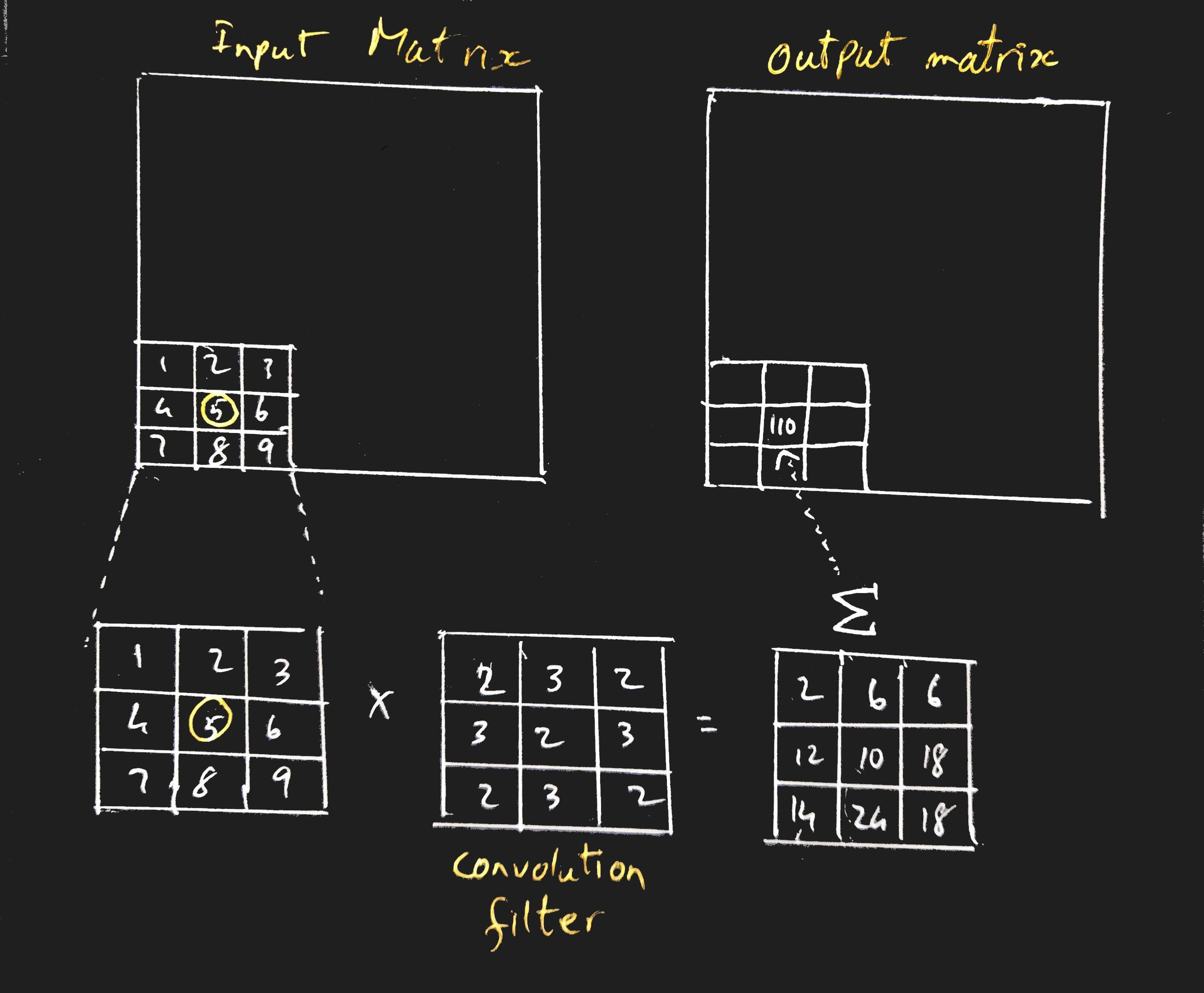
For my purposes, convolution is this: For each input element in a 2D matrix of size NxN, apply a
function on it that takes that input element and some of its neighboring
elements (so your input to the function is a smaller nxn matrix with your input
element at the center), multiplies this smaller matrix by a another known nxn matrix
called a convolution kernel or convolution filter and sums these multiplied elements together to
produce one output element. The width of a convolution filter is 2r+1 where
r is the radius of the filter. In the below example, we have a filter of
radius r=1.
This type of operation is done a lot in image processing. For example one way to blur an image: for each input pixel of an image, take its surrounding pixels so you have a 3x3 grid of pixels with your input pixel at the center, then multiply this by another grid that looks like this:
0.11|0.11|0.11
----|----|----
0.11|0.11|0.11
----|----|----
0.11|0.11|0.11then sum the values together to get the new pixel value for the output. Doing this for each pixel will blur the image. Our grid of 0.11s is our convolution filter .
Here’s a short Python program that does this
#!/usr/bin/env python
# coding: utf-8
from PIL import Image
import functools
input_image = Image.open("grace_hopper.jpg")
input_pixels = input_image.load()
width, height = input_image.size
convolution_filter = [
0.11, 0.11, 0.11,
0.11, 0.11, 0.11,
0.11, 0.11, 0.11
]
output_image = Image.new("RGB", input_image.size)
output_pixels = output_image.load()
for i in range(1, width-1):
for j in range(1, height-1):
pixel_grid = [
input_pixels[i-1,j-1], input_pixels[i, j-1], input_pixels[i+1, j-1],
input_pixels[i-1,j], input_pixels[i, j], input_pixels[i+1, j],
input_pixels[i-1,j+1], input_pixels[i, j+1], input_pixels[i+1, j+1],
]
# for each pixel in pixel grid (which is a tuple (R, G, B)), multiply its RGB values with the value in the convolution filter
modified_inputs = map(lambda x,y: [int(x*yi) for yi in y], convolution_filter, pixel_grid)
# sum all the modified input pixels (adding up the values of the R, G, and B) to produce the output pixel
output_pixel = functools.reduce(lambda x,y: (x[0]+y[0], x[1]+y[1], x[2]+y[2]), modified_inputs)
output_pixels[i, j] = output_pixel
output_image.save("grace_hopper_blurred.jpg")And here’s the original picture of Grace Hopper and the one that is now a little blurry.


(This is a super contrived example because 0.11 is basically 1⁄9, so you’re multiplying your 3x3 pixel grid centered on your input pixel with a grid of 1⁄9 s and then summing your grid. This is no different from taking the average of the values in the 3x3 pixel grid for each input pixel. But I wanted to demonstrate this because your convolution filter could be anything, not just a grid of 0.11s).
Anyway now that I’ve explained what convolution is, let’s look at programming it for a GPU.
A simple algorithm for convolution on GPU is to start a number of blocks and threads such that you have one thread for each output element of your 2D matrix. The thread will be responsible for taking the nxn grid of the input elements, multiplying it with the convolution filter, and summing it to produce the output element. This can be made more efficient if all the threads in the block work together to load an input tile of elements into shared memory to save on redundant memory accesses (I discuss this in more detail in my blog post on corner turning).
However, there’s a couple of things to keep in mind. If you’re calculating the output element you need the nxn input element grid, so you need to make sure your tile contains those input elements. So the number of output elements calculated from the inputs in the tile is going to be less than the number of inputs in the tile. You can’t calculate the output element for an input element that is at the border of a tile since that would require the surrounding input elements, some of which lie outside of the tile.
Say we had the below input tile loaded by the threads in the block (the block is sized such that it is the same size as the input tile, and one thread loads one element into the input tile) and our filter radius was 1 (so the filter size would 3x3, and the required input grid would also be 3x3). To calculate the output element for the corresponding input element that is at the corner, we would need additional input elements from around it to form the input grid. But those don’t exist. So we can’t calculate that output element. We can calculate the output of the inner elements in the tile, but not those at the border. The distance from the border of the input tile must be equal to the filter radius or more for the output element to not require any input elements that lie outside the tile.
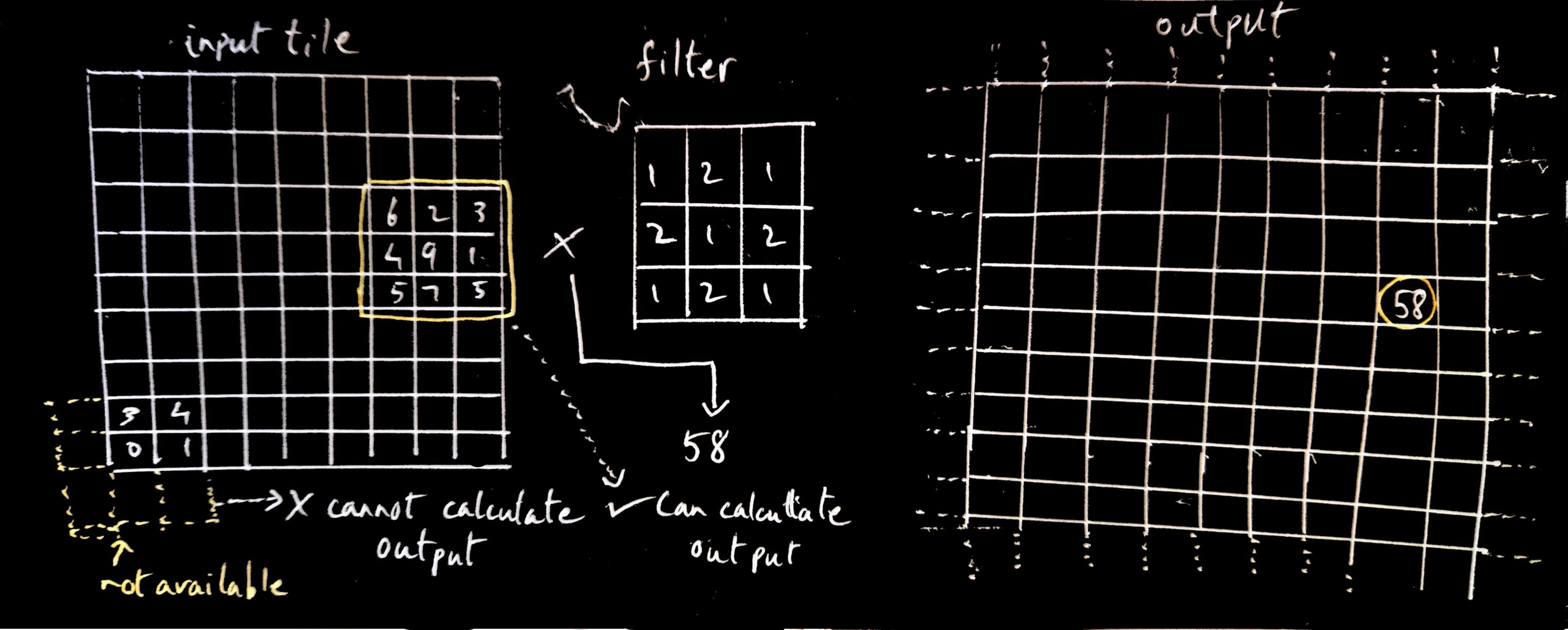
So this means that after the tile is loaded into shared memory, some threads in the block will be inactive since they are not going to be calculating any output element.
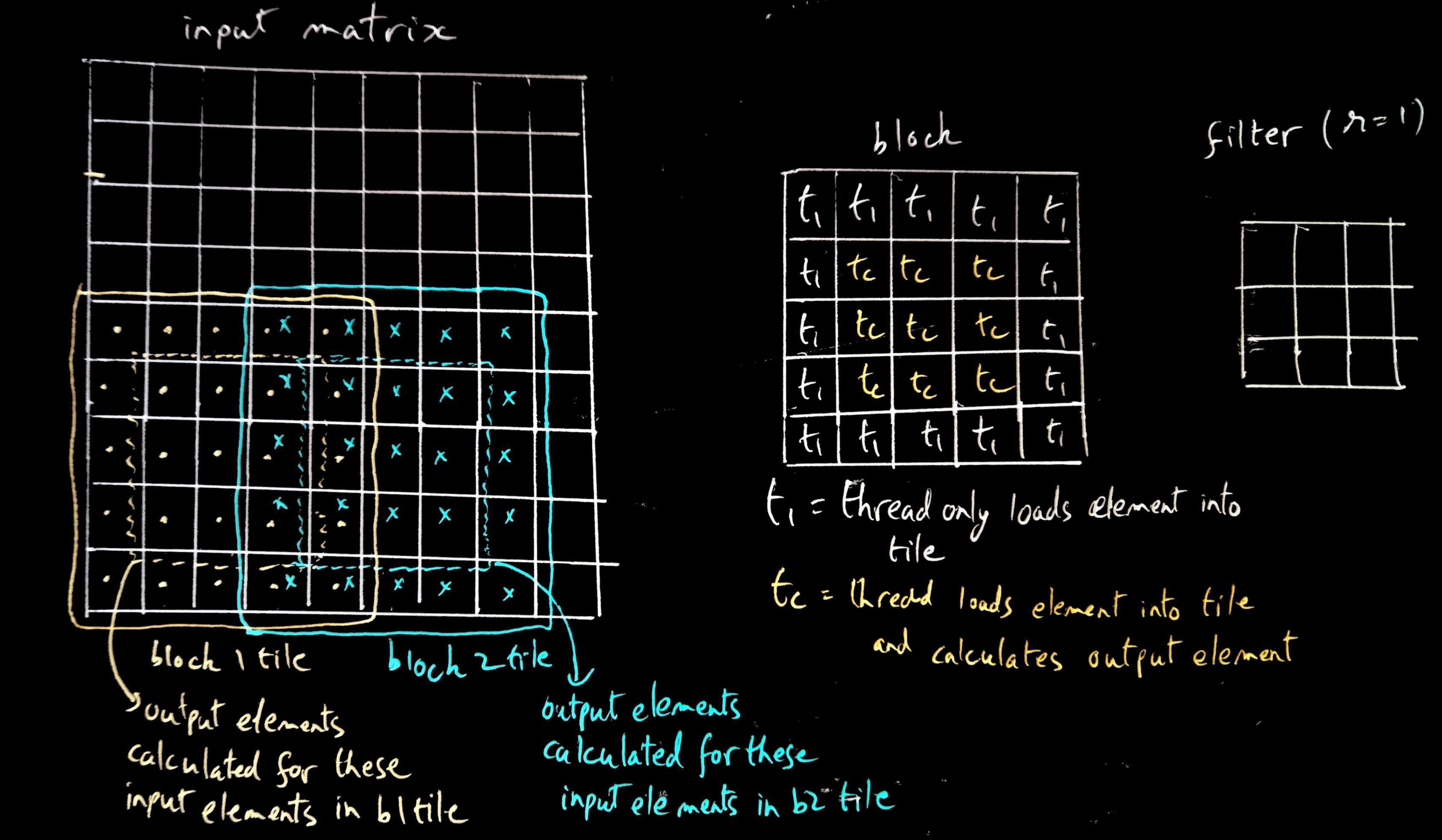
Another thing is that when the input matrix is being divided up among the blocks to load as tiles, there needs to be some slight overlap between the tiles loaded by different blocks so that the output elements that can’t be calculated by one block (because the elements are at the border of the tile) will be calculated by a neighboring block that includes those elements and enough of its surrounding elements.
In the below image, we have a filter of radius 1 (so filter size is 3x3), each block is 5x5 threads so it will load a 5x5 input tile into shared memory. The neighboring block will load an input tile that will overlap with the elements loaded by the previous block so that those output elements that cannot be calculated by the first block will be calculated by the second block. In this overlapping manner, several blocks are created that will cover the whole input matrix.
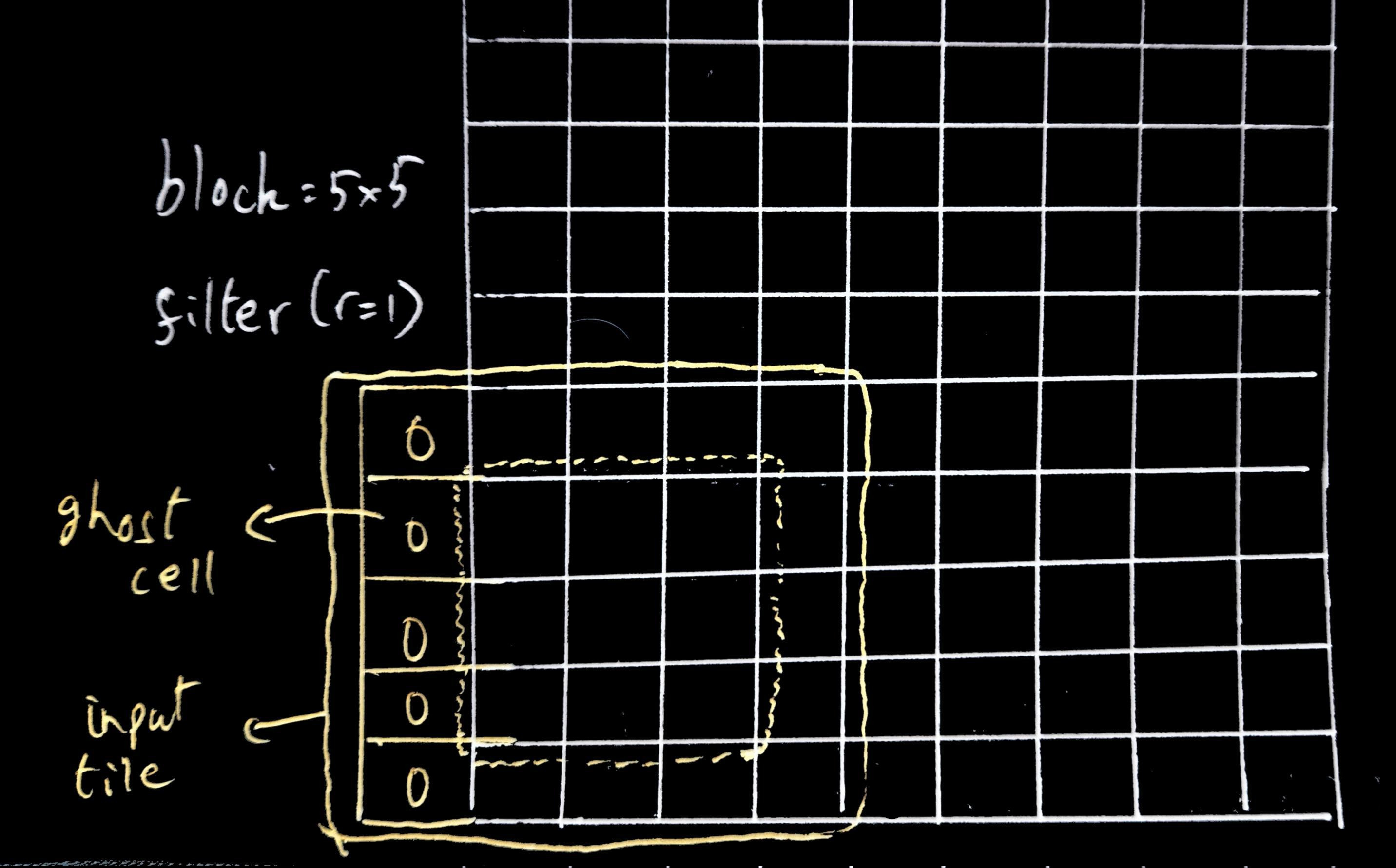
One more thing to keep in mind is that there needs to be a way to calculate the output elements for inputs that are on the borders of the input matrix. However, there are no input elements beyond the border of the actual input matrix that also need to be loaded for the output elements on the border to be calculated. So what do you do? The solution there is to use some default value like 0 instead. A block loading an input tile when it sees it needs to load an element outside the bounds of the input matrix, will instead set that value in the input tile to 0 or some other default value. These are called ghost cells.
In general, the element loaded by a thread in a block into an input tile is determined by
FILTER_RADIUS = f
# INPUT_TILE_DIM is the size of input tile and also the block size
INPUT_TILE_DIM = D
# OUTPUT_TILE_DIM is the size of the subset of the input tile elements for which we can
# actually calculate the output elements for, given the input tile.
# Here basically we are moving inward away from the borders by FILTER_RADIUS amount
OUTPUT_TILE_DIM = INPUT_TILE_DIM = INPUT_TILE_DIM-(2*FILTER_RADIUS)
# because each block calculates the output of the OUTPUT_TILE_DIM subset, each
# next block must start at OUTPUT_TILE_DIM distance from the previous block,
# then step backward by FILTER_RADIUS amount to get necessary input elements
# from the input matrix loaded into the input tile that are needed to calculate the output.
# blockIdx.(x|y) * OUTPUT_TILE_DIM is the starting point of the next set of
# elements for which the output will be calculated. -FILTER_RADIUS sets that
# starting point back to the starting point from which the input tile should be loaded
# in order have enough surrounding elements for the output elements to be
# calculated. threadIdx.(x|y) gives the offset from this starting point at which
# the input element will be loaded by this particular thread.
col = blockIdx.x * OUTPUT_TILE_DIM + threadIdx.x - FILTER_RADIUS
row = blockIdx.y * OUTPUT_TILE_DIM + threadIdx.y - FILTER_RADIUSWhere each input tile loaded by a block starts and which output elements are calculated given the input tile is a little hard to visualize. So I have a Jupyter Notebook that visualizes this. You can download it here or open it at this Binder link.
With all of this hand, you can convolve the whole input matrix given the convolution filter.
(Of course, later I learn that instead of doing this complicated way of having an input tile and then calculating output for only a subset of elements in the input tile because you don’t have all the input elements needed in the input tile, you can instead simply not worry about it. Instead you can load up the input tile, and if you want to calculate the output of an element at the border of the input tile, then just read the required surrounding input elements from the input matrix directly if they’re not in the input tile. This is relying on the GPU’s caching mechanism where multiple threads might try to load that same element from outside the tile so it will be cached, counteracting any performance penalty you might see from having to read from the input matrix directly instead of from the tile in shared memory.)
I should also note that the convolution I describe above also works for 1D and 3D matrices, I’m just using 2D matrices for my example for ease of explanation.